Let It Grow Sunday!
This week's game is called Grow.

Draw each item to the center of the ball to Grow it. If you drag them in the right order you will reach the maximum growth level for each object -- that's the challenge and it's not easy. ;-) Lots of trial and error. The number of different ways to play this game is 479 001 600. Can you find the winning strategy?
The Applied Math class will learn how to figure this out this week. Pre-Cal will learn it in about two more months and the AP Calculus students should remember from the Pre-Cal class. Do you?
Have Fun!

Draw each item to the center of the ball to Grow it. If you drag them in the right order you will reach the maximum growth level for each object -- that's the challenge and it's not easy. ;-) Lots of trial and error. The number of different ways to play this game is 479 001 600. Can you find the winning strategy?
The Applied Math class will learn how to figure this out this week. Pre-Cal will learn it in about two more months and the AP Calculus students should remember from the Pre-Cal class. Do you?
Have Fun!
 For the last trial, the king used not two, nor three, but nine rooms! The prisoner was told that one room contained a Lady and the other eight were either empty or filled with a tiger. The sign on the Lady's door was true, the signs on room with tigers were false, and empty rooms had signs that were either true or false.
For the last trial, the king used not two, nor three, but nine rooms! The prisoner was told that one room contained a Lady and the other eight were either empty or filled with a tiger. The sign on the Lady's door was true, the signs on room with tigers were false, and empty rooms had signs that were either true or false.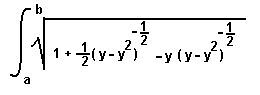 You can find a good review with a little practice on antiderivatives
You can find a good review with a little practice on antiderivatives 



